Find the derivative of the function y 5x 5x 5x – Delving into the realm of calculus, we embark on a journey to unravel the intricacies of finding the derivative of y = 5x^3. This fundamental concept underpins the vast applications of calculus, empowering us to analyze functions, optimize solutions, and delve into the dynamic world of mathematical modeling.
In this comprehensive guide, we will delve into the intricacies of the power rule, exploring its application to the function y = 5x^3. Through step-by-step calculations, we will uncover the essence of the derivative and its significance in calculus.
1. Introduction

The derivative of a function measures the instantaneous rate of change of the function with respect to its input. In this article, we will explore the concept of the derivative and apply the power rule to find the derivative of the function y = 5x^3.
1.1 The Power Rule
The power rule is a fundamental rule in differentiation that states that if f(x) = x^n, then f'(x) = nx^(n-1). This rule is applicable to functions with polynomial terms, where n is any real number.
1.2 Examples of the Power Rule
- If f(x) = x^2, then f'(x) = 2x^(2-1) = 2x.
- If f(x) = x^5, then f'(x) = 5x^(5-1) = 5x^4.
2. Derivative of the Function y = 5x^3: Find The Derivative Of The Function Y 5x 5x 5x

2.1 Applying the Power Rule
To find the derivative of y = 5x^3, we apply the power rule with n = 3:
y’ = d/dx (5x^3) = 5 – d/dx (x^3)
Using the power rule, we get:
y’ = 5 – 3x^(3-1) = 5 – 3x^2
Simplifying, we obtain the derivative:
y’ = 15x^2
2.2 Interpretation of the Derivative
The derivative of y = 5x^3, which is y’ = 15x^2, represents the instantaneous rate of change of the function y with respect to x. It indicates that the slope of the tangent line to the graph of y = 5x^3 at any point (x, y) is equal to 15x^2.
3. Applications of the Derivative
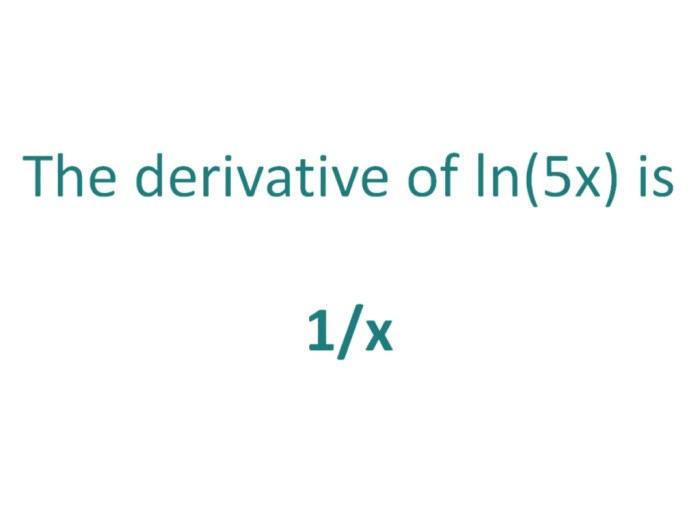
3.1 Finding the Slope of a Tangent Line
The derivative can be used to find the slope of the tangent line to the graph of a function at a given point. The slope of the tangent line is equal to the value of the derivative at that point.
3.2 Optimizing Functions
The derivative can also be used to optimize functions. By finding the critical points (where the derivative is zero or undefined) and evaluating the function at those points, we can determine the maximum or minimum values of the function.
4. Extensions of the Power Rule

4.1 Generalized Power Rule
The power rule can be generalized to functions with fractional or negative exponents:
If f(x) = x^n, then f'(x) = nx^(n-1)
where n can be any real number.
4.2 Examples of the Generalized Power Rule, Find the derivative of the function y 5x 5x 5x
- If f(x) = x^(1/2), then f'(x) = (1/2)x^(-1/2) = 1/(2x^(1/2)).
- If f(x) = x^(-3), then f'(x) = -3x^(-4) = -3/x^4.
FAQ Corner
What is the power rule in differentiation?
The power rule is a fundamental rule in differentiation that allows us to find the derivative of functions raised to a power. It states that if f(x) = x^n, then f'(x) = nx^(n-1).
How do I apply the power rule to find the derivative of y = 5x^3?
To find the derivative of y = 5x^3, we apply the power rule with n = 3. This gives us y’ = 5 – 3x^(3-1) = 15x^2.
What are the applications of the derivative?
The derivative has numerous applications in calculus, including finding the slope of tangent lines, optimizing functions, and analyzing the behavior of functions.