Embarking on the realm of geometry 10.3 practice a answers, this comprehensive guide unlocks the fundamental concepts and practical applications of geometry. Delving into the intricacies of geometric shapes, relationships, and theorems, this exploration empowers learners to tackle practice problems effectively and unravel the real-world significance of geometry.
Through a systematic approach, we unravel the complexities of angles, lines, and planes, laying the groundwork for problem-solving strategies. Theorems and postulates become tools for constructing geometric proofs, enabling learners to navigate the intricacies of geometric reasoning. Moreover, we illuminate the diverse applications of geometry in fields such as architecture and engineering, showcasing its indispensable role in shaping our world.
Geometry Concepts
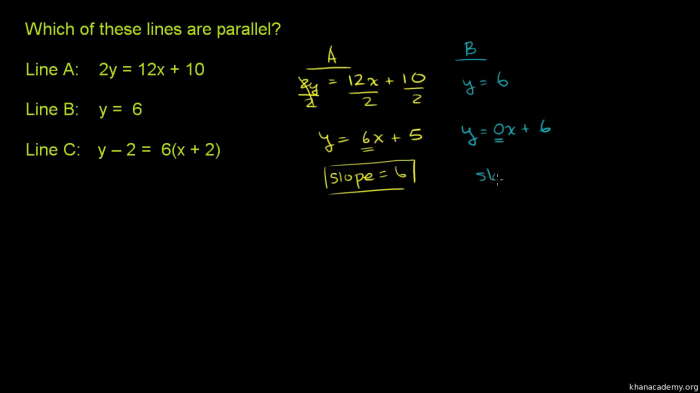
Geometry 10.3 Practice A explores fundamental concepts in geometry, including points, lines, planes, angles, and geometric shapes. Points represent specific locations in space, while lines extend infinitely in one dimension and planes extend infinitely in two dimensions. Angles are formed by two intersecting lines, and geometric shapes are two-dimensional figures bounded by lines or curves.
Examples of geometric shapes include triangles, squares, circles, and spheres. Triangles are three-sided polygons with three angles, squares are four-sided polygons with four right angles, circles are closed curves with all points equidistant from a central point, and spheres are three-dimensional shapes with all points equidistant from a central point.
Geometry also explores the relationships between angles, lines, and planes. For instance, the sum of the interior angles of a triangle is always 180 degrees, parallel lines never intersect, and a plane is determined by any three non-collinear points.
Practice Problems
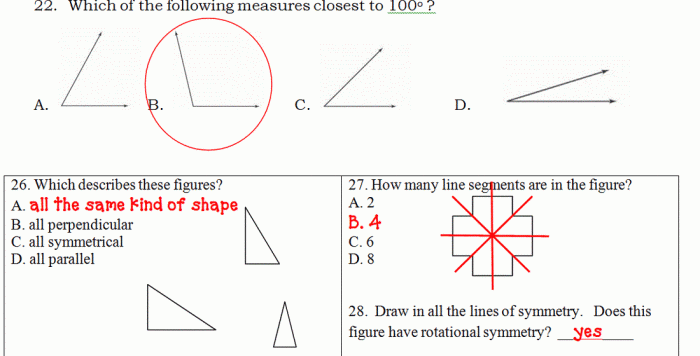
Geometry 10.3 Practice A includes various types of practice problems designed to reinforce the concepts covered in the lesson. These problems may involve:
- Identifying geometric shapes and their properties
- Measuring angles and distances
- Drawing and constructing geometric figures
- Solving problems involving relationships between angles, lines, and planes
- Applying geometric theorems and postulates
To solve these problems effectively, students should:
- Understand the relevant geometric concepts
- Use appropriate tools and techniques, such as rulers, protractors, and compasses
- Draw accurate diagrams to visualize the problem
- Apply logical reasoning and problem-solving skills
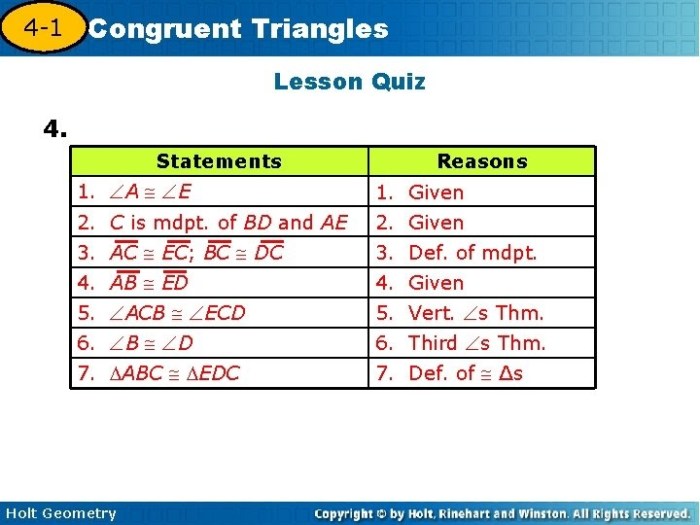
Theorems and Proofs
Geometry 10.3 Practice A introduces several important theorems and postulates, including:
- Triangle Sum Theorem
- Angle Bisector Theorem
- Parallel Line Theorem
- Perpendicular Bisector Theorem
These theorems provide a foundation for solving geometric problems. Students should understand the statements of these theorems and be able to apply them to solve problems. They should also be able to construct geometric proofs using these theorems.
To construct a geometric proof, students should:
- Start with the given information
- Apply relevant theorems and postulates
- Draw a logical conclusion
- State the proof in a clear and concise manner
Applications of Geometry: Geometry 10.3 Practice A Answers
Geometry has numerous real-world applications in various fields, including:
- Architecture: Designing and constructing buildings and structures
- Engineering: Designing and building bridges, roads, and machines
- Art: Creating paintings, sculptures, and other works of art
- Science: Understanding the physical world and developing scientific models
- Everyday life: Measuring distances, estimating quantities, and solving spatial problems
By understanding geometry, individuals can better appreciate the world around them and make informed decisions in various aspects of life.
Essential FAQs
What types of practice problems are included in Geometry 10.3 Practice A?
Geometry 10.3 Practice A encompasses a range of practice problems, including angle measurement, triangle congruence, and circle properties.
How can I effectively solve practice problems in Geometry 10.3?
To effectively solve practice problems, focus on understanding the underlying concepts, applying relevant theorems, and utilizing problem-solving strategies.
What are the key theorems used in Geometry 10.3 Practice A?
Geometry 10.3 Practice A utilizes theorems such as the Pythagorean Theorem, Angle Bisector Theorem, and Triangle Sum Theorem.